e per GNU/linux:
http://newbufferedwriter.blogspot.com/2013/11/calcolare-il-determinante-di-una_18.html
Era da tempo che mi volevo cimentare in un programma del genere. Per il corso di elettrotecnica avevo sviluppato un programma in C# per calcolare il determinante di una matrice 3x3, che mi è servito per calcolare la soluzione ai sistemi di equazioni per i circuiti; ma comunque era limitato solamente a matrici 3x3.
Ho pensato pochi giorni fa di implementare un programma del genere con la ricorsione. Dalla matematica "pratica" sappiamo che calcolare il determinante per matrici di grosse dimensioni è complesso, specialmente se si usa la definizione fondamentale del determinante. Io in questo programma ho usato lo sviluppo di Laplace avete questa forma:
che come si può notare, la formula stessa è ricorsiva, ovvero il determinante compare nell'espressione stessa. det Mij è il determinante della matrice estrapolata dalla matrice originale escludendo la riga i e la colonna j, quindi in definitiva l'ordine diminuisce di 1 ad ogni ricorsione. Quando si "ferma" la ricorsione? Semplice: quando la matrice raggiunge l'ordine 2, che, essendo una matrice elementare, è possibile con un'espressione elementare (non più ricorsiva) calcolare il suo determinante.
Facciamo un esempio. Consideriamo la seguente matrice di ordine 3:
| 2 8 6 |
| 4 5 2 |
| 1 7 4 |
Il suo determinante si può calcolare in questo modo:
1)Scegliamo una riga (per esempio la riga 1: {2,8,6}). Di solito nella pratica si sceglie una riga con molti zeri, ma in questo caso non ci sono zeri; e comunque ci dobbiamo mettere nei panni del calcolatore, che prende sempre e comunque la riga 1 per questo programma che ho creato.
2)Moltiplichiamo ogni elemento della riga per il suo complemento algebrico (ovvero il determinante della matrice ottenuta eliminando la riga 1 e la colonna del singolo elemento)
3)Addizioniamo i 3 risultati trovati, avendo cura di preporre ad ogni singolo elemento il segno, negativo o positivo che sia (Delta di Kronecker, in questo caso poitivo se la colonna è dispari, negativo se è pari).
| 2 8 6 |
det | 4 5 2 | = 2 * det | 5 2| - 8 * det | 4 2| + 6 * det | 4 | 5 | = 2 * (5*4-2*7) -
| 1 7 4 | |7 4| | 1 4| | 1 | 7 |
- 8*(4*4-2*1) + 6 *(4*7-5*1) = 2*6 - 8*14 + 6*23 = 38
Il seguente programma scirtto in C++ fa la stessa cosa per matrici di qualsiasi dimensione. Ho definito la funzione det che accetta come parametri la matrice (ovvero un doppio puntatore a interi) e il suo ordine. Nel metodo main ho inserito per esempio la matrice che abbiamo analizzato, ma potete crearne voi una qualsiasi.
#include <iostream>
using namespace std;
int det(int**,int);
int main(){
int** m;
m = new int*[3]; //ordine 3, alloco il primo vettore
for (int i=0;i<3;i++) //alloco gli altri vettori
m[i] = new int[3];
m[0][0]=2;m[0][1]=8;m[0][2]=6;
m[1][0]=4;m[1][1]=5;m[1][2]=2;
m[2][0]=1;m[2][1]=7;m[2][2]=4;
int deter = det(m,3);
cout << "Il determinante e': " << deter;
}
int det(int** matrice,int ordine){
if (ordine==2)
return (matrice[0][0]*matrice[1][1] - matrice[0][1]*matrice[1][0]);
else {
int provv=0; //risultato "provvisorio", ovvero diventa definitivo quando la ricorsione termina
bool col=false; //variabile utile per creare la sottomatrice
bool segnoNegativo = false; //variabile che tiene conto del simbolo di Kronecker
int elem;
for (int i=0;i<ordine;i++){ //colonna
int** matrix;
/*ALLOCO MEMORIA PER LA NUOVA MATRICE*/
matrix = new int*[ordine-1];
for (int c=0;c<ordine-1;c++)
matrix[c] = new int[ordine-1];
/*---------------FINE----------------*/
for (int r=1;r<ordine;r++){ //inizio a creare la nuova matrice
for (int c=0;c<ordine;c++){
if (c==i) {
col = true;
c++; //salta questa colonna e vai avanti
if (c==ordine) //controllo per non fare eccedere i limiti
break;
}
if (col)
matrix[r-1][c-1] = matrice[r][c];
else
matrix[r-1][c] = matrice[r][c];
}
col=false;
} //Fine r
if (segnoNegativo)
elem = -matrice[0][i];
else
elem = matrice[0][i];
provv += elem * det(matrix,ordine-1);
segnoNegativo = !(segnoNegativo);
} //fine i
return provv;
} //fine else
}
using namespace std;
int det(int**,int);
int main(){
int** m;
m = new int*[3]; //ordine 3, alloco il primo vettore
for (int i=0;i<3;i++) //alloco gli altri vettori
m[i] = new int[3];
m[0][0]=2;m[0][1]=8;m[0][2]=6;
m[1][0]=4;m[1][1]=5;m[1][2]=2;
m[2][0]=1;m[2][1]=7;m[2][2]=4;
int deter = det(m,3);
cout << "Il determinante e': " << deter;
}
int det(int** matrice,int ordine){
if (ordine==2)
return (matrice[0][0]*matrice[1][1] - matrice[0][1]*matrice[1][0]);
else {
int provv=0; //risultato "provvisorio", ovvero diventa definitivo quando la ricorsione termina
bool col=false; //variabile utile per creare la sottomatrice
bool segnoNegativo = false; //variabile che tiene conto del simbolo di Kronecker
int elem;
for (int i=0;i<ordine;i++){ //colonna
int** matrix;
/*ALLOCO MEMORIA PER LA NUOVA MATRICE*/
matrix = new int*[ordine-1];
for (int c=0;c<ordine-1;c++)
matrix[c] = new int[ordine-1];
/*---------------FINE----------------*/
for (int r=1;r<ordine;r++){ //inizio a creare la nuova matrice
for (int c=0;c<ordine;c++){
if (c==i) {
col = true;
c++; //salta questa colonna e vai avanti
if (c==ordine) //controllo per non fare eccedere i limiti
break;
}
if (col)
matrix[r-1][c-1] = matrice[r][c];
else
matrix[r-1][c] = matrice[r][c];
}
col=false;
} //Fine r
if (segnoNegativo)
elem = -matrice[0][i];
else
elem = matrice[0][i];
provv += elem * det(matrix,ordine-1);
segnoNegativo = !(segnoNegativo);
} //fine i
return provv;
} //fine else
}
In sintesi, cosa fa il programma, in particolare la funzione int det(int** matrice,int ordine); ?
1)Per prima cosa controlla l'ordine. Se è due, restituisce immediatamente il risultato, altrimenti continua.
2)Crea una matrice di ordine ordine-1 e la inizializza con la sottomatrice (col è una variabile boolean utile per sapere qual'è la colonna a cui appartiene l'elemento).
3)Procede per aggiungere alla variabile provv (inizializzata a zero) il prodotto del singolo elemento per il suo complemento algebrico (ovvero una nuova chiamata alla stessa funzione det(); qui sta la ricorsione), tenendo conto del segno tramite la variabile boolean segnoNegativo.
4)Finito il ciclo della variabile temporanea i, restituisce il risultato (provv).
Analizziamo cosa succede in memoria. Il caso di ordine 3 è abbastanza semplice perché necessita di 3 cicli ed una sola ricorsione. La memoria della matrice di ordine 3-1 = 2 viene liberata alla fine di ogni ciclo ma comunque ad ogni ricorsione si accumula, quindi in definitiva per questo caso la massima memoria utilizzata contemporaneamente è quella per memorizzare una matrice 3x3 e una 2x2, ovvero rispettivamente 48 e 24 byte, quindi 48+24 = 72byte. Per una matrice di ordine 4 la massima memoria utilizzata contemporaneamente è quella per memorizzare una matrice 4x4, una 3x3 e una 2x2, ovvero rispettivamente 80 + 48 + 24 = 152. L'espressione della memoria occupata da una matrice di ordine n è:
4 * (n^2 + n)
in questo modo ho stilato una tabella che ci indica quanta memoria viene utilizzata dal programma al crescere dell'ordine n:
n | Max memoria(byte)
--|---------------------
2| 24
3| 72
4| 152
5| 278
6| 440
7| 664
8| 952
9| 1312
10| 1752
Tutto ciò era solamente per uno scopo goliardico...comunque sia la memoria utilizzata non è poi tanta...no?
Alberto
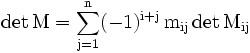
secondo me è un gran programma
RispondiElimina